Exact Solution of Uda Equation (6) @ Quantum History Theory @ Products @ Forum @ www.GrammaticalPhysics.ac

since 2006
Help　Sitemap

< Forum >

< Products >

< Quantum History Theory >

< Exact Solution of Uda Equation (6) >

In this page, I write exact solutions of Uda Equation in case of V = 0.

.
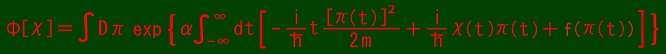where f: R → C.

Φ[χ(□ - ε)] = ∫Dπ exp{α∫_-∞^∞dt[-(i/h)tπ(t)²/(2m) + f(π(t))]} exp[(i/h)α∫_-∞^∞dt'π(t')χ(t' - ε)]
　= ∫Dπ exp{α∫_-∞^∞dt[-(i/h)tπ(t)²/(2m) + f(π(t))]} exp[(i/h)α∫_-∞^∞dt'π(t' + ε)χ(t')]
　= ∫Dπ' exp{α∫_-∞^∞dt[-(i/h)tπ'(t - ε)²/(2m) + f(π'(t - ε))]} exp[(i/h)α∫_-∞^∞dt'π'(t')χ(t')]
　= ∫Dπ' exp{α∫_-∞^∞dt[-(i/h)(t + ε)π'(t)²/(2m) + f(π'(t))]} exp[(i/h)α∫_-∞^∞dt'π'(t')χ(t')]
where π'(t) = π(t + ε).

ih lim_ε→0 (1/ε) {Φ[χ(□ - ε)] - Φ[χ]}
　= ∫Dπ' {α∫_-∞^∞dt[π'(t)²/(2m)]} exp{α∫_-∞^∞dt[-(i/h)(t + ε)π'(t)²/(2m) + f(π'(t))]} exp[(i/h)α∫_-∞^∞dt'π'(t')χ(t')].

{α∫_-∞^∞dt[-(ih/α)δ/δχ(t)]²/(2m)]}Φ[χ]
　= ∫Dπ' {α∫_-∞^∞dt[π(t)²/(2m)]} exp{α∫_-∞^∞dt[-(i/h)tπ(t)²/(2m) + f(π(t))]} exp[(i/h)α∫_-∞^∞dt'π(t')χ(t')].

∴ ih lim_ε→0 (1/ε) {Φ[χ(□ - ε)] - Φ[χ]} = {α∫_-∞^∞dt[-(ih/α)δ/δχ(t)]²/(2m)]}Φ[χ].

∫_-∞^∞dp exp{α∫_a^{a +ε}dt[-(i/h)tp²/(2m) + (i/h)xp + f(p)]} (ε→ +0)
　=∫_-∞^∞dp exp{αε[-(i/h)ap²/(2m) + (i/h)xp + f(p)]}
　= exp{αεf([-ih/(αε)]∂/∂x)} ∫_-∞^∞dp exp{αε[-(i/h)ap²/(2m) + (i/h)xp]}
　= exp{αεf([-ih/(αε)]∂/∂x)} √{π/[αε(i/h)a/(2m)]}・exp{(-1/h²)α²ε²x²/[4αε(i/h)a/(2m)]}
　= √[2mhπ/(iαεa)]・exp{αεf([-ih/(αε)]∂/∂x)} exp{[imαε/(2ha)]x²}.

If f(p) = 0, ψ(x, t) = exp{[im/(2h)](x²/t)}.

If f(p) = kp,
∫_-∞^∞dp exp{αε[-(i/h)ap²/(2m) + (i/h)xp + f(p)]}
= ∫_-∞^∞dp exp[αε{-(i/h)ap²/(2m) + [(i/h)x + k]p}]
= c exp{αε[(i/h)x + k]²/[4(i/h)a/(2m)]}
= c exp{αε[im/(2h)](x - ihk)²/a}
∴ ∫Dπ exp{α∫_a^a+1/αdt[-(i/h)tπ(t)²/(2m) + (i/h)xπ(t) + f(π(t))]}
　　≒ c'[∫_-∞^∞dp exp{αε[-(i/h)ap²/(2m) + (i/h)xp + f(p)]}]^1/(αε)
　　= c''exp{[im/(2h)](x - ihk)²/a}.

If f(p) = -K(p - b)²,
∫_-∞^∞dp exp{αε[-(i/h)ap²/(2m) + (i/h)xp + f(p)]}
= ∫_-∞^∞dp exp{-αε[K + (i/h)a/(2m)]p² + αε[(i/h)x + 2bK]p - αεKb²}
= C exp{αε(1/4)[(i/h)x + 2bK]²/[K + (i/h)a/(2m)]}
= C exp{αε(-1/2)(m/h)(x - 2ihbK)²/(2hmK + ia)}
∴ ∫Dπ exp{α∫_a^a+1/αdt[-(i/h)tπ(t)²/(2m) + (i/h)xπ(t) + f(π(t))]}
　　≒ C'[∫_-∞^∞dp exp{αε[-(i/h)ap²/(2m) + (i/h)xp + f(p)]}]^1/(αε)
　　= C''exp{-(1/2)(m/h)(x - 2ihbK)²/(2hmK + ia)}.

I can not calculate for general f but I assume that the following functional integral converges except for constant factor for wide variety of f.
∫Dπ exp{α∫_a^a+1/αdt[-(i/h)tπ(t)²/(2m) + (i/h)xπ(t) + f(π(t))]}.

Any superposition of solutions of the form at the top of this page is also a solution.
It is as follows.

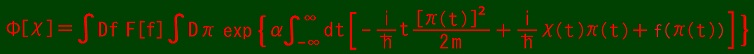
where F is an arbitrary complex valued functional.
This perhaps covers all general solutions.

---

The original form of the solution shown in this page started being displayed at the top of this page at 2019/11/11/21:05JST.
It was of the same meaning as the meaning of the present form though it was transformed into the present form later.
Gaussian integration was done on 2019/11/15.

Author Yuichi Uda, Write start at 2019/11/11/20:15JST, Last edit at 2019/12/06/17:13JST