
since 2006
Help Sitemap
In this page, I write exact solutions of Energy Representation of Uda Equation (1).
Any unentangled solution is functional Φ such that

where ∀n ∈ Z; cn ∈ C.
The quantum history represented by this solution is the same history as represented by wave function ψ such that
ψ(n, t) = exp(-iωtn + cn) = λn exp(-iωnt)
in the old grammar.
Here, λn ≡ exp(cn).
If A†A|n> = n|n>, Σn=0∞ ψ(n, t)|n> = Σn=0∞ λnexp(-iωnt)|n>, Σn=0∞ ψ(n, 0)|n> = Σn=0∞ λn|n>.
Of course, any superposition of unentangled solutions is also a solution.
Moreover, any entangled solution perhaps is a superposition of unentangled solutions.
It is functional Φ such that
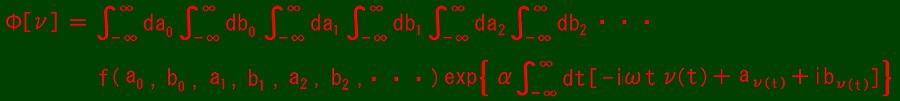
where ∀n ∈ Z; an ∈ R and bn ∈ R and f(a0, b0, a1, b1, a2, b2, ・・・) ∈ C.
cn = an + ibn, λn = exp(an + ibn).
Normalization condition for initial state is that
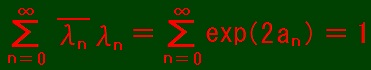 .
.To let the integral converge, b and ν is restricted.
However, I do not put such a condition because there is no ambiguity even if the integral diverges.
---
The content of this page was developed in Number Representation of Uda Equation @ Quantum History Theory @ Problems.