
since 2006
Help Sitemap
I wonder if the difficulty that an unentangled solution does not exist in position representation is not physical contents but mere a problem of expression.
Condition x ≠ 0 ⇒ δ(x) = 0 in the definition of Dirac's delta function is analogous to the condition that a quantum state is not entangled.
Condition ∫-∞∞dx δ(x) = 1 in the definition of Dirac's delta function is analogous to the Uda equation.
So, an unentangled solution of Uda equation may exist as something like Dirac's delta function.
Then I try making energy representation to take a shortcut without a problem of expression.
As for a harmonic oscillator, energy representation is number representation.
So, here I try writing number representation of a harmonic oscillator to learn about energy representation.
A harmonic oscillator is defined as a classical system with Hamiltonian H such that
H(x, p) = [1/(2m)]p2 + (mω2/2)x2.
A quantum mechanical harmonic oscillator is defined by quantizing the classical harmonic oscillator.
Definition of it is the following set of conditions.
X† = X, P† = P,
[X, P]- ≡ XP - PX = i
H = [1/(2m)]P2 + (mω2/2)X2 -
i
Here I used the fact that Hamiltonian may be shifted by an arbitrary real number term.
By introducing A such that
A ≡ {√[(mω)/(2
H is rewritten as
H =
Eigenvalues of A†A are 0, 1, 2, 3, ・・・.
So, let us put Uda equation as follows.
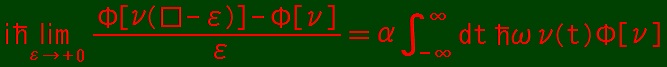
where ν: R → {0, 1, 2, 3, ・・・}.
The idea of Uda equation is seen in Uda Equation.
⊿a,ε(t) ≡ 0 if t < a or t ≧ a + ε.
⊿a,ε(t) ≡ 1 if a ≦ t < a + ε.
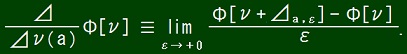
Reduced form of Uda equation is as follows.
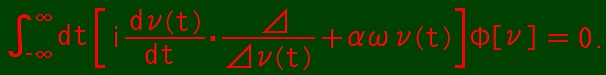
The idea of reduced form of Uda equation is seen in Reduced Form of Uda Equation and Uda Equation of Fermionic Mechanics.
The formulation made in this page should be criticized at the point that energy or quantum state might be not defined at infinitely short time moment.
ν(t) is number of bosons and it has no counterpart in the classical mechanics.
So, the formulation in this page might be not fully new grammatical one but thought of as a compromise between old and new quantum grammar.
---
The content of this page was developed in Number Representation of Uda Equation @ Quantum History Theory @ Problems.