since 2006 Help　Sitemap
	< Forum >
		< Products >
			< Quantum History Theory >
				< Uda Equation >
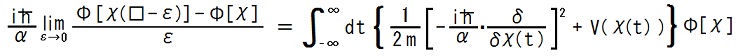
					A functional Φ representing an entangled quantum history obeys the new grammar version of Schrödinger equation: 　 where α is a new physical constant with the dimension of (time)-1 introduced by Yuichi Uda and χ(□-ε) is a function defined as ∀t∈R; [χ(□-ε)](t) = χ(t-ε). This equation describes the physical law for a particle with mass m in one-dimensional space. V is a function representing a potential energy. I named this equation Uda equation. --- I found the Uda equation by the following schematic deduction which is an application of the correspondence principle. Φ[χ] = Πkφ(χ(kε), kε)　[Mnew(Φ) = Mold(φ)] ih(∂/∂t)φ(x, t) = H(x, -ih∂/∂x)φ(x, t) ・・・ the schrödinger equation as an old equation (1/ε){Φ[χ(□-ε)] - Φ[χ]} = (1/ε){Πkφ(χ(kε-ε), kε) - Πkφ(χ(kε), kε)} = (1/ε){Πkφ(χ((k-1)ε), kε) - Πkφ(χ(kε), kε)} = (1/ε){Πsφ(χ(sε), (s + 1)ε) - Πkφ(χ(kε), kε)}　(s=k-1) = (1/ε){Πsφ(χ(sε), sε+ε) - Πsφ(χ(sε), sε)} = Σk[Πs≠kφ(χ(sε), sε)](∂/∂t)φ(χ(kε), t)|t=kε　(product rule) = (ih)-1Σk[Πs≠kφ(χ(sε), sε)]H(x, -ih∂/∂x)φ(x, t)|x=χ(kε), t=kε = (ih)-1ΣkH(χ(kε), -ih∂/∂χ(kε))Πsφ(χ(sε), sε) = (ihε)-1εΣkH(χ(kε), -ih∂/∂χ(kε))Φ[χ] → (ihε)-1∫dt H(χ(t), -ihεδ/δχ(t))Φ[χ]　　[εΣk→∫dt, ∂/∂χ(kε)→εδ/δχ(t)] ∴ (ihε)(1/ε){Φ[χ(□-ε)] - Φ[χ]} = ∫dt H(χ(t), -ihεδ/δχ(t))Φ[χ] By setting ε for 1/α in the above result, we see the Uda equation as a new equation. --- This article is a rewrite of the article 'New Grammar Version of Schrödinger Equation' in the following page. Former half@Theory of Quantum History Entangled in Time-like Direction@Products of Grammatical Physics@Grammatical Physics@Forum@Vintage(2008-2014) The content of this article was presented by me at APS+JPS 2006 Autumn Meeting. --- The Uda equation was first thought out in the following articles written in the Japanese language. メッセージ19, 20 @ 13-27 @ 時間の量子化 @ 中心問題解決案 @ 文法レベルでの自然 @ Japanese @ Vintage(2005-2008) These were written on 2005/06/03.
				Author Yuichi Uda, Write start at 2015/05/21/20:52JST, Last edit at 2016/04/05/20:16JST